Электродинамическое действие токов КЗ

Способность аппаратов, проводников и изоляторов противостоять электродинамическим и термическим воздействиям, возникающим при прохождении через них наибольших токов КЗ, называют соответственно электродинамической и термической стойкостью.

При КЗ с достаточной для практики точностью процесс нагрева можно принять адиабатическим:

,

где i_k (t) — функция, характеризующая изменение тока КЗ во времени; R _J — сопротивление проводника при данной температуре J; C_J — удельная теплоемкость проводника при данной температуре; G — масса проводника.

Учитывая, что сопротивление проводника и его удельная теплоемкость являются функциями температуры:

,

где r ₀ и с₀ — удельные сопротивление и теплоемкость проводника при начальной температуре J _н=0 °С; a и b — температурные коэффициенты сопротивления и теплоемкости; S, l, g — площадь поперечного сечения, длина и плотность проводника.

Разделяя переменные и интегрируя в требуемых пределах, получаем уравнение

которое позволяет определить конечную температуру проводника J_к при нагреве его током КЗ от начальной температуры J _н. Однако аналитическое решение этого уравнения сложно, и поэтому для распространенных проводниковых материалов построены зависимости значений второго интеграла от конечной температуры (при J _н=0), которые представлены на рис. 2.8.

Рис. 2.8. Кривые для определения температуры нагрева токоведущих частей при КЗ

Первый интеграл, зависящий от тока КЗ и времени отключения t _откл, получил название импульса квадратичного тока КЗ В. Его приближенное значение может быть выражено через действующие значения полного тока и его составляющих

Где — действующее значение полного тока КЗ в момент времени t; I _{п, t} — действующее значение периодической составляющей; i_а,t — апе­риодическая составляющая.

Таким образом, импульс квадратичного тока КЗ равен сумме импульсов от периодической B _п и апериодической B _а составляющей.

Импульс от периодической составляющей можно определить графоаналитическим методом путем замены плавной кривой ступенчатой с ординатами, соответствующими средним значениям квадратов действующих значений токов для каждого интервала времени :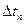

.

В тех случаях, когда место замыкания удалено от генераторов или требуется грубо (с завышением) оценить импульс от периодической составляющей, можно принять, что периодическая составляющая не затухает, т. е. и .

Импульс от апериодической составляющей тока КЗ равен:

.

При находим

.

Тогда конечная температура проводника будет равна

.

На рис. 2.8 откладываем по оси ординат J_н и по соответствующей кривой (точка а) находим А _н. Прибавляя к А _н (на оси абсцисс) величину B / S ², получаем А _н и отвечающую ей температуру проводника J_к (точка б на кривой).

Конечная температура при КЗ не должна быть выше допускаемой по условию сохранения изоляции или по условию механической прочности (для неизолированных проводников).

Условие термической стойкости проводника:

;

.

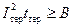Термическую стойкость аппаратов принято характеризовать номинальным током термической стойкости I _тер при определенной длительности его прохождения, называемой номинальным временем термической стойкости t _тер. Для проверки аппарата на термическую стойкость сопоставляют нормированное заводом изготовителем значение теплового импульса с расчетным. Условие термической стойкости аппарата формулируется в виде:

.

Методика расчета термической и динамической стойкости проводников и аппаратов боле подробно приведена в руководящих указаниях по расчету токов короткого замыкания и выбору электрооборудования РД 153–34.0–20.527–98

Электродинамическая стойкость определяется механическими напряжениями в материале проводников и изоляторов, которые не должны быть выше допускаемых напряжений, но последние нормируются по-разному, а именно:

для токоведущих шин

;

опорных изоляторов

;

аппаратов

,

где s _{max, расч} — максимальное расчетное напряжение в материале шин, МПа; s_доп — допускаемое напряжение в материале шин (для алюминия марки AT s_доп =70 МПа, стали s_доп=160 МПа); F _расч — расчетная электродинамическая сила, приложенная в головке изолятора, Н; F _разр — минимальная разрушающая сила (нагрузка) на изгиб, Н (задается заводом-изготовителем); I _{дин, max} — номинальный ток электродинамической стойкости аппарата, кА; I _{уд, max} — ударный ток КЗ при повреждении в расчетной точке, кА.

Обычно для аппаратов I _{дин, max} задают заводы, а у петлевых и стержневых трансформаторов тока нормируется кратность электродинамической стойкости . Для выключателей по ГОСТ 687–70 нормируется сквозной предельный ток, определяемый начальным действующим значением его периодической составляющей I _п0.

Для расчета электродинамической стойкости шин необходимо, прежде всего, найти величины и выяснить характер действующих сил.

Если два параллельных тонких и прямолинейных проводника 1 и 2 расположены в одной плоскости на расстоянии а и обтекаются токами , то результирующая сила, действующая на участке проводника 1 длиной l (например между опорными изоляторами), будет равна:

где плюс берется при одинаковом направлении токов i ₁, i ₂ (сила стремится сблизить проводники), минус — при разном (сила стремится удалить проводники).

Соответственно этому при двухфазном КЗ () получаем

.

Наибольшие электродинамические силы действуют на среднюю фазу (расположение шин в одной плоскости) при трехфазном КЗ и поэтому принимаются за расчетные:

.

В последнем выражении множитель обусловлен фазовым сдвигом между взаимодействующими токами, а коэффициент формы k _ф учитывает геометрию проводников и их взаимное расположение. Его величина может быть больше или меньше единицы в зависимости от формы поперечного сечения шин и их взаимного расположения.

Если считать шину многопролетной балкой, лежащей на жестких опорах и подвергающейся воздействию равномерно распределенной статической нагрузки, то в этих условиях наибольший изгибающий момент, Н×м действущий на шину, определяют по формуле

Напряжение в материале шин, МПа,

где W — момент сопротивления шины относительно оси, перпендикулярной направлению действия силы, м³.

Сила, действующая на шины от начала КЗ до его отключения, переменна. Вместе с тем конструкция шин является механически упругой системой, обладающей собственной частотой колебаний. Если частота вынуждающей силы и собственная частота колебаний упругой системы будут близки или совпадут, то возникнут условия для механического резонанса, в результате которого напряжения в материале шин увеличатся и возможно разрушение конструкции.

Дата добавления: 2015-05-08; Просмотров: 2335; Нарушение авторских прав?; Мы поможем в написании вашей работы!